lara091

Новичок
|
      
функция общих издержек фирмы соответствует функции TC=Q^2+5Q+25. Выразить функции переменных т, постоянных, средних и предельных издержек
|
Всего сообщений: 2 | Присоединился: ноябрь 2011 | Отправлено: 7 нояб. 2011 19:20 | IP
|
|
Anya111


Новичок
|
      
Помогите пожалуйста, если не сложно(((
1. Определить коэффициент прямой эластичности спроса по цене (Ed-?), если известно, что функция спроса на товар (Qd=15-2p),а цена (Р) = 6 у.е. за единицу товара.
2.Ф-ция спроса на товар Х представлена в виде Qdx=10-Px+0.5Py.
Определить коэфф. перекрестной эластичности спроса на товар Х, если цена товара Х=12 у.е. , а товара У=8 у.е.
|
Всего сообщений: 2 | Присоединился: ноябрь 2011 | Отправлено: 7 нояб. 2011 19:43 | IP
|
|
Sokratus


Долгожитель
|
      
Цитата: lysik lysik написал 7 нояб. 2011 1:15
здравствуйте! снова я со своей задачей.просто чего то недопонимаю помогите пожалуйста!!!!
Фирма, которая продает диваны, повысила цену от 940 до 980 гривен. Объем продаж уменьшился со 120 до 100 диванов в месяц. Обозначьте эластичность спроса на этот товар.
решение
Т.к. неизвестна форма зависимости между объемом спроса и ценой, то необходимо рассчитать коэффициент дуговой эластичности: дуговая Edp = (Q1 - Q0)/(P1 - P0)*(P1 + P0)/(Q1 + Q0) = (980 - 940)/(100 - 120)*(100 + 120)/(980 + 940) = -2*0,115 = -0,23.
вот вы мне ее решили, спасибо огромное. но я никак не могу выйти на тот ответ =-0,23!!!!!!!!! у меня получается - 0,33 . это эластичный спрос или нет? и почему!?за ранее благодарна
Сейчас все еще раз пересчитал дважды. В формуле я уверен. Результат опять равен (-0,23)  . .
(980 - 940)/(100 - 120)*(100 + 120)/(980 + 940) = -40/20*220/1920 = -2*0,115.
Т.к. величина коэффициента находится в промежутке от (-1) до 0, то это неэластичный спрос.
|
Всего сообщений: 599 | Присоединился: декабрь 2008 | Отправлено: 8 нояб. 2011 5:03 | IP
|
|
Sokratus


Долгожитель
|
      
Цитата: malinka написал 4 нояб. 2011 4:56
Помогите пожалуйста решить задачу.На сессию задали, а я вообще без понятия как решать!
МС=300+49Q
P=650-20Q
Нужно найти:ТС,МС,МR,Общий доход и экономическую прибыль.
TC = VC + FC, VC - это первообразная функции MC.
VC = 300Q + 24.5Q^2. Т.к. значение FC нам не дано, то принимаем его равным 0. Тогда, TC = VC = 300Q + 24.5Q^2.
Чтобы рассчитать значения указанных величин необходимо использовать правило максимизации прибыли фирмой-несовершенным конкурентом MC = MR.
MR = a - 2bQ для обратной функции спроса вида P = f(Q). MR = 650 - 40Q. Тогда:
300 + 49Q = 650 - 40Q; 89Q = 350; Qe = 4. Подставляя в функцию спроса, получаем Pe = 650 - 20*4 = 610.
TC = 300*4 + 24.5*4^2 = 1592; MC = 300 + 49*4 = 496; MR = 650 - 40*4 = 490 (разница между MC и MR обусловлена округлением при расчете Qe); TR = Pe*Qe = 610*4 = 2440; П = TR - TC = 2440 - 1592 = 848.
P.S.: На всякий случай пересчитайте математику.
|
Всего сообщений: 599 | Присоединился: декабрь 2008 | Отправлено: 8 нояб. 2011 5:23 | IP
|
|
Sokratus


Долгожитель
|
      
Цитата: lara091 написал 7 нояб. 2011 21:04
функция общих издержек фирмы соответствует функции TC=Q^2+5Q+25. Выразить функции переменных т, постоянных, средних и предельных издержек
FC = 25 (константа в функции TC), VC = Q^2+5Q (переменная часть в функции TC), AC = TC/Q = Q + 5 + 25/Q; MC есть первая производная функции TC, т.е. MC = (TC)` = 2Q +5.
|
Всего сообщений: 599 | Присоединился: декабрь 2008 | Отправлено: 8 нояб. 2011 5:27 | IP
|
|
Sokratus


Долгожитель
|
      
Цитата: Anya111 написал 7 нояб. 2011 21:43
Помогите пожалуйста, если не сложно(((
1. Определить коэффициент прямой эластичности спроса по цене (Ed-?), если известно, что функция спроса на товар (Qd=15-2p),а цена (Р) = 6 у.е. за единицу товара.
2.Ф-ция спроса на товар Х представлена в виде Qdx=10-Px+0.5Py. Определить коэфф. перекрестной эластичности спроса на товар Х, если цена товара Х=12 у.е. , а товара У=8 у.е.
1. Используем так называемую "формулу расстояний": Ed = -P/ (Pmax - P), где Pmax – значение цены по функции спроса при Q = 0.
Найдем Pmax: 15 – 2Р = 0; Pmax = 7,5.
Ed = - 6/(7,5 - 6) = -4.
(Проверка методом углового коэффициента: Ed = -b*P/Q, где b – модуль коэффициента угла наклона в прямой функции спроса вида Qd = a - bP; Q (P = 6) = 3; Ed = -2*6/3 = -4.)
2. Подставив в имеющуюся функцию значение цены Px = 12 у.е., приведем ее к более удобному виду Qdx = 10 - Px + 0,5Py = 10 - 12 + 0,5Py = -2 + 0,5Py. Т.к. функция имеет положительный наклон, то использовать «формулу расстояний» нельзя. Поэтому применим метод углового коэффициента:
Qdx (Py = 8) = -2 + 0,5*8 = 2 ед.;
|Ed| = 0,5*8/2 = 2.
Знак коэффициента определяем следующим образом: т.к. функция имеет положительный наклон, то товары x и y являются субститутами (с ростом цены y растет спрос на x), следовательно, коэффициент должен быть со знаком плюс. Т.о, Ed = 2.
P.S.: В решении задачи 2 не уверен. В обоих задачах обязательно самостоятельно проверьте расчеты!
|
Всего сообщений: 599 | Присоединился: декабрь 2008 | Отправлено: 8 нояб. 2011 5:45 | IP
|
|
Sokratus


Долгожитель
|
      
Цитата: fmaik написал 3 нояб. 2011 18:00
Sokratus, большая просьба помочь. Буду премного благодарен.
№1
Монополия, максимизирующая прибыль, может продавать продукцию на двух сегментах рынка. Имеющих следующие функции спроса q(1)=100-2P(1) и q(2)=60-2P(2). Функция общих затрат монополии имеет вид: ТС=18Q; q(1)+q(2)=Q.
А) Какую прибыль получит монополия при проведении ценовой дискриминации?
Б) По каким ценам монополия будет продавать продукцию и сегментах рынка и какие объемы?
№2
Функция спроса на некоторый товар имеет вид: Q(Dt)=150-P(t). Функция предложения данного товара: Q(St)=-15+0.5P(t), где P(t) – цена товара в период t, которую ожидают производители в момент принятия решений об объемах производства. Предположим, что P(t)=P(t-1).
А) определить объемы продаж и цены данного товара в периода 1, 2, 3, 4, если известно, что P(0)=100.
Б) Определить равновесную цену и равновесный объем продаж.
В) Можно ли равновесие назвать стабильным?
P.S. Все что в скобках подстрочные символы.
№1
Условие максимизации прибыли фирмы-монополиста, осуществляющей ценовую дискриминацию, в данном случае можно записать следующим образом: MR(q1) = MR(q2) = MC. Рассчитаем соответствующие функции.
MC есть первая производная функции TC: MC = (TC)` = (18Q)` = 18.
Для нахождения функций MR используем формулу MR = a – 2bqn, где a и b – коэффициенты в обратных линейных функция спроса вида P = a – bqn. Для этого выразим функции спроса в виде обратных:
q1 = 100 – 2P1; 2P1 = 100 – q1; P1 = 50 – 0,5q1;
q2 = 60 – 2P2; 2P2 = 60 – q2; P2 = 30 – 0,5q2.
Тогда соответствующие функции MR можно представить как: MR(q1) = 50 – q1; MR(q2) = 30 – q2.
Равновесные показатели по сегментам и для рынка в целом находим из решения системы следующих уравнений:
50 – q1 = 18;
30 – q2 = 18;
q1 + q2 = Q.
Следовательно,
-q1 = 18 – 50 = -32; q1 = 16;
-q2 = 18 – 30 = -12; q2 = 6;
Q = 16 + 6 = 32.
Прибыль по сегментам определяем по формуле Пn = TRn – TC(qn) = Pn*Qn - TC(qn):
П1 = (50 – 0,5q1)*q1 – 18q1 = (50 – 0,5*16)*16 – 18*16 = 672 – 288 = 384;
П2 = (30 – 0,5q2)*q2 – 18q2 = (30 – 0,5*6)*6 – 18*6 = 162 – 108 = 54.
Общая прибыль составляет П = П1 + П2 = 384 + 54 = 438.
Ответ: А) П = 438; Б) P1 = 50 – 0,5q1 = 50 – 0,5*16 = 42, q1 = 16; P2 = 30 – 0,5q2 = 30 – 0,5*6 = 27, q2 = 6.
№2
В задаче рассматривается так называемая паутинообразная модель рыночного равновесия.
А) Т.к. по условию задачи P(t) = P(t-1), то объем выпуска в момент времени t = 1 находим, подставляя цену P(0) = 100 в функцию предложения: Q(1) = -15 + 0,5P(0) = -15 + 0,5*100 = 35.
Цену периода t = 2 определяем из функции спроса по условию Q(2) = Q(1) = 35:
35 = 150 – P(2); P(2) = 150 – 35 = 115.
Объем выпуска в момент времени t = 3 находим из условия P(3) = P(2) = 115, Подставляя таковую в функцию предложения: Q(3) = -15 + 0,5*115 = 42,5.
Цену периода t = 4 определяем из функции спроса по условию Q(4) = Q(3) = 42,5:
42,5= 150 – P(4); P(4) = 150 – 42,5= 107,5.
Б) Равновесные параметры определим из условия Qd = Qs:
150 – P = -15 + 0,5P; -1,5P = -165; Pe = 110; Qe = 150 – 110 = 40.
В) Покажем полученные значения на графике:
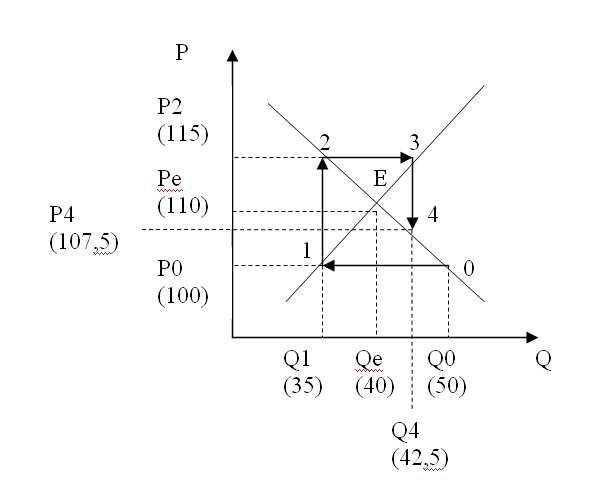
Как следует из графика, параметры рыночной конъюнктуры по периодам приближаются к равновесным величинам. Т.о., равновесие является стабильным.
(Проверка. Согласно теории рыночное равновесие является устойчивым, если для обратных функций спроса и предложения вида Pd(t) = a – bQ(t), Ps(t-1) = m +nQ(t), соответственно, выполняется условие |b| > n, где |b| и n – коэффициенты угла наклона соответствующих функций.
Выведем обратные функции спроса и предложения:
Qd=150 – P; Pd = 150 – Q и
Qs = -15 + 0,5P; -0,5P = -15 – Qs; Ps = 30 + 2Qs.
Следовательно, |b| = 1 < n = 2, т.е. равновесие является неустойчивым, что противоречит графическому анализу).
P.S.: Все расчеты в задаче 2 проверял трижды. В чем ошибка, не вижу.
(Сообщение отредактировал Sokratus 8 нояб. 2011 12:52)
|
Всего сообщений: 599 | Присоединился: декабрь 2008 | Отправлено: 8 нояб. 2011 8:36 | IP
|
|
lysik lysik

Новичок
|
      
Сократус! огромное спасибо! вы не представляете какое доброе дело делаете для людей!. простите что я вас так с этой задачей снова утруждала. это я бестолковая! 100+120 у меня получалось 100, поэтому не могла никак выйти на результат -0,23!!дурка я! еще раз спасибо большое выручаете людей!
|
Всего сообщений: 18 | Присоединился: ноябрь 2011 | Отправлено: 8 нояб. 2011 12:21 | IP
|
|
Sokratus


Долгожитель
|
      
Да я сам иногда ошибаюсь в элементарных вычислениях, когда на автомате считаю  . Так что я бы не удивился, если бы в расчете обнаружил ошибку. . Так что я бы не удивился, если бы в расчете обнаружил ошибку.
И спасибо за теплые слова!
|
Всего сообщений: 599 | Присоединился: декабрь 2008 | Отправлено: 8 нояб. 2011 13:03 | IP
|
|
lysik lysik

Новичок
|
      
бывает. просто не допоняла. и подумала что лучше спрошу еще раз! смотрю вы всегда отзываетесь на просьбы. спаисбо огромнейшее! я теперь первая решила контрольную работу! и у меня 5 ! спасибо допуск к зачету есть!. только вот не понимаю , какая вам выгода это все делать бесплатно? извините, не мое дело..но манит интерес!
|
Всего сообщений: 18 | Присоединился: ноябрь 2011 | Отправлено: 8 нояб. 2011 13:10 | IP
|
|
|

 Форум
Форум

 Экономика
Экономика

 Микроэкономика
Микроэкономика

 Форум
Форум

 Экономика
Экономика

 Микроэкономика
Микроэкономика