Разложение силы на две составляющие

(Физика → Теоретическая механика → Плоская система сходящихся сил → Задача 26)

Условие задачи

Между высокими стенами необходимо временно подвесить некоторый груз весом 140 кГ на одинаковом расстоянии по 1 м от стен и на высоте 1 м от горизонтального пола. Имеются два куска каната по несколько метров длины каждый. Один из канатов с учетом безопасности подвески можно нагрузить усилием не более 70 кн, а второй – усилием не более 100 кн.

На какой высоте над полом необходимо укрепить концы канатов, чтобы после подвески к ним груза в заданном положении усилия в канатах не превышали допускаемых 70 и 100 кн?

<< задача 25 || задача 27 >>

Решение 1 (графическим методом по правилу параллелограмма)

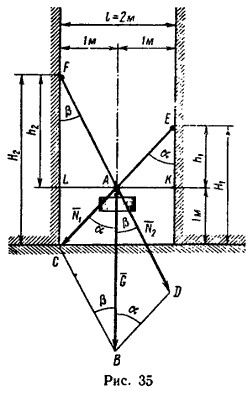
Рис. 35. Подвешенный на канатах груз

1. Выбираем масштаб построения так, что длина 1 м изображается на чертеже отрезком, равным 12,5 мм (1 м в 12,5 мм):
μl = 1 м / 12,5 мм = 0,08 м/мм
и строим две вертикальные стены и горизонтальный пол (рис. 35).

В выбранном масштабе расстояние l=2 м между стенами на чертеже изобразим отрезком, равным
1/μl = 2 м / 0,08 м/мм = 25 мм*.

На расстоянии 1 м от пола и по 1 м от стен отмечаем точку А, в которой должен быть подвешен груз.

1. Выбираем масштаб сил μсил=4 кн/мм (4 кн в 1 мм длины). Значит груз G=140 кн изобразится отрезком
AB = G/μсил = 140/4 = 35 мм.

Отложим этот отрезок из точки А на чертеже.

По условию задачи, усилие в канатах не должно быть больше N1=70 кн и N2=100 кн. Эти усилия в выбранном масштабе изобразятся отрезками
AC = N1/μсил = 70/4 = 17,5 мм,
AD = N2/μсил = 100/4 = 25 мм.

Сделав при помощи циркуля засечки радиусами, равными этим длинам, сначала из точки A, а затем из точки В получим параллелограмм ACBD.

3. Усилия N1 и N2 должны действовать вдоль канатов, поэтому, продлив отрезок СА до пересечения с правой стеной, получим на ней точку E – место закрепления одного каната и, продлив отрезок DA, получим на левой стене точку F – место закрепления второго каната.

4. Измерив на чертеже расстояние от точки Е до линии пола, получим 25 мм, значит точка закрепления первого каната должна находиться от пола на расстоянии, не меньшем
H1 = 25 мм * 0,08 м/мм ≈ 2.

Измерив расстояние от точки F до линии пола, получим 36 мм. Значит точка закрепления второго каната должна находиться от пола на расстоянии, не меньшем
H2 = 36 мм * 0,08 м/мм ≈ 2,9 м.

Для большей безопасности подвески, если позволяют длины кусков канатов, обе точки их закрепления можно поднять выше. Усилия в канатах при этом уменьшатся.

Решение 2 (графо-аналитическим методом по правилу параллелограмма)

1. Для графо-аналитического решения нужно также выполнить чертеж без соблюдения точного масштаба. Воспользуемся рис. 35, на котором ясно видно, что искомые расстояния можно получить как суммы

Определение положения канатов

Сравнив результаты, полученные в решении 2, с результатами графического решения, увидим, что они практически совпадают.

* Описываемое в тексте построение рекомендуется воспроизвести на листе бумаги, но в ином масштабе, например 0,04 м/мм или 0,02 м/мм.