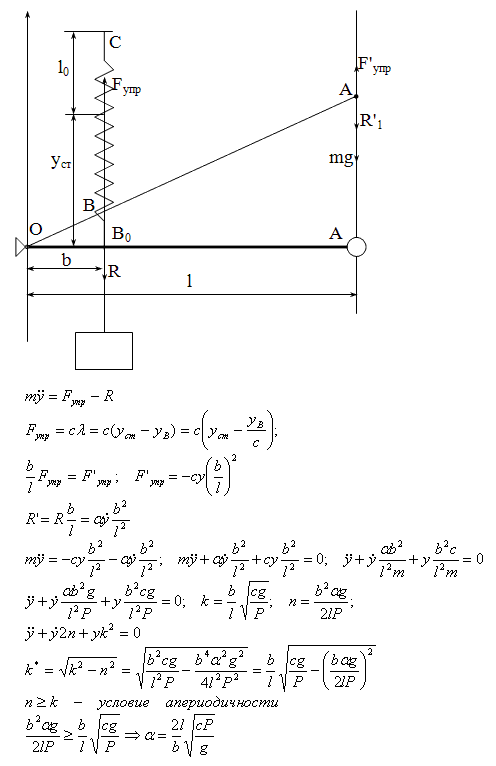
Решение задачи 32.74 из сборника Мещерского по теоретической механике

(Физика → Термех → Решебник Мещерского → Динамика материальной точки → Колебательное движение)

Условие задачи

Составить дифференциальное уравнение малых колебаний тяжелой точки A, находящейся на конце стержня, закрепленного шарнирно в точке О, считая силу сопротивления среды пропорциональной первой степени скорости с коэффициентом пропорциональности α, и определить частоту затухающих колебаний. Вес точки A равен P, коэффициент жесткости пружины c, длина стержня l, расстояние OB=b. Массой стержня пренебречь. В положении равновесия стержень горизонтален. При каком значении коэффициента α движение будет апериодическим?