Разложение силы на две составляющие

(Физика → Теоретическая механика → Плоская система сходящихся сил → Задача 27)

Условие задачи

На конце В стержня АВ, длина которого AB=l, шарнирно прикрепленного в точке А к вертикальной стене, необходимо подвесить груз весом G=6 кн, причем стержень АВ должен образовывать со стеной угол 45° (рис. 36, а). На каком расстоянии Н от точки А необходимо прикрепить трос СВ, удерживающий стержень в заданном положении, если трос может быть нагружен усилием не более 4,5 кн? Определить также усилие, возникшее в стержне АВ после подвески к нему груза.

<< задача 26 || задача 33 >>

Решение (графо-аналитическим методом по правилу параллелограмма)

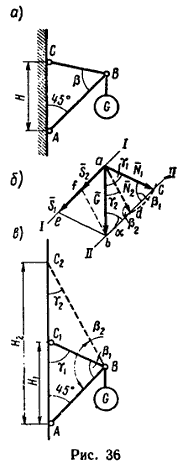
Рис. 36. Трос, удерживающий шарнирное крепление

1. Из произвольной точки a в произвольном масштабе проведем отрезок ab который изобразит вектор G – вес груза (рис. 36, б).

Так как стержень АВ должен занимать положение под углом 45° к вертикальной стенке, то усилие S в этом стержне будет направлено под углом 45° к направлению G. Проведем из точек a и b вектора G параллельные прямые под углом α=45° к линии действия вектора G (линии I-I и II-II).

Если теперь из точки a отложить вектор, численно равный усилию N=4,5 кн, максимально допустимому в тросе ВС (см. рис. 36, а), то увидим, что этот отрезок пересечет линию II—II в двух точках – в точках c и d. Проделав ту же операцию из точки b, получим два параллелограмма: первый acbe и второй adbf.

Это значит, что задача допускает бесчисленное множество решений*. При одном и том же направлении усилия S в стержне АВ трос может быть направлен к стержню под углом β, но не менее β1 и не более β2, (β1≤β≤β2).

Определение положения троса

* В предельном случае, если уменьшим заданное допускаемое усилие в тросе, задача может иметь одно решение (дуга cd, проведенная из a, касается линии II-II). При дальнейшем уменьшении допускаемого усилия в тросе задача практически неосуществима.