MEHT


Долгожитель
|
    
Мне думается, что приравнивать к нулю ускорение было бы неправильным. Соотношение a = А - ВV² уже само по себе задаёт закон движения, поскольку ускорение представляет собой производную по времени от скорости.
От этого равенства и станцуем.
Для нахождения скорости следует решить дифференциальное уравнение

(точкой обозначено дифференцирование по времени t; параметры A и B заменил строчными буквами, дабы смотрелось неброско)
Его можно сразу же и проинтегрировать, разделив переменные
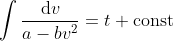
и, покуда a и b положительны,
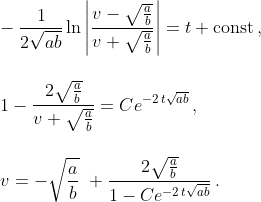
Константу C выражаем из условия равенства нулю начальной скорости v(0)=0; в этом случае C=-1 и закон скорости
=-%5Csqrt{%5Cfrac{a}{b}}%20%5C%20+%20%5Cfrac{2%5Csqrt{%5Cfrac{a}{b}}}{1%20+%20e^{-2%5C,t%5Csqrt{ab}}}%5C,.)
Вы можете видеть, что экспонента при больших временах будет давать ничтожно малое значение, поэтому скорость почти постоянна. Однако строгого постоянства скорости начиная с некоторого момента времени после начала движения (что свидетельствовало бы об обнулении ускорения) нет.
(Сообщение отредактировал MEHT 16 апр. 2012 9:00)
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 16 апр. 2012 8:52 | IP
|
|
and27

Новичок
|
    
А путь тогда найти через диф уравнение, расписав время как dV/dt?
|
Всего сообщений: 23 | Присоединился: апрель 2012 | Отправлено: 16 апр. 2012 9:42 | IP
|
|
MEHT


Долгожитель
|
    
Нет. Нужно проинтегрировать v=v(t) по времени:
=%5Cint%5Climits_{0}^{t}v%5Cleft%20(%20%5Ctau%20%5Cright%20)d%5Ctau%20=%20-%5Csqrt{%5Cfrac{a}{b}}%5C%20t%20%5C%20+%20%5C,%20%5Cfrac{1}{b}%20%5C,%20%5Cln%5Cleft%20(%20%5Cfrac{1+e^{2%5C,t%5Csqrt{ab}}}{2}%20%5Cright%20)%20=%20%5Csqrt{%5Cfrac{a}{b}}%5C%20t%20%5C%20+%20%5C,%20%5Cfrac{1}{b}%20%5C,%20%5Cln%5Cleft%20(%20%5Cfrac{1+e^{-2%5C,t%5Csqrt{ab}}}{2}%20%5Cright%20))
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 16 апр. 2012 11:10 | IP
|
|
MEHT


Долгожитель
|
    
Перепроверьте на всякий случай. Невзначай мог и ошибится.
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 16 апр. 2012 11:12 | IP
|
|
and27

Новичок
|
    
А можно остановиться на втором выражении, когда у нас есть зависимость времени от скорости и найти константу?
|
Всего сообщений: 23 | Присоединился: апрель 2012 | Отправлено: 16 апр. 2012 11:43 | IP
|
|
and27

Новичок
|
    
Если в начальный момент времени t=0, то и путь должен быть раен нулю. Но из последнего выражения путь равен некоторой величине. Она ничтожна мала, если b большое число, но тем немение...прокоментируйте.
|
Всего сообщений: 23 | Присоединился: апрель 2012 | Отправлено: 16 апр. 2012 12:49 | IP
|
|
MEHT


Долгожитель
|
    
Цитата: and27 написал 16 апр. 2012 11:43
А можно остановиться на втором выражении, когда у нас есть зависимость времени от скорости и найти константу?
А какой смысл? Это константа в промежуточных выкладках. Цель была найти скорость как функцию времени, разрешив соответствующее диф. уравнение.
Цитата: and27 написал 16 апр. 2012 12:49
Если в начальный момент времени t=0, то и путь должен быть раен нулю. Но из последнего выражения путь равен некоторой величине. Она ничтожна мала, если b большое число, но тем немение...прокоментируйте.
А он нулю и равен  С чего Вы взяли что это не так? С чего Вы взяли что это не так?
В первом члене понятно - он линеен по t; во втором члене экспонента в нулевой степени даст единицу, всё выражение под знаком логарифма следовательно тоже единица, ну а логарифм единицы 0.
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 16 апр. 2012 15:55 | IP
|
|
MEHT


Долгожитель
|
    
Вы спрашивали:
Если ускорение тела непостоянно и имеет закон изменения а = А - ВV² (V - в квадрате). Как здесь определить время при котором движение станет равномерным и какой путь при это тело пройдет?
Ответ следует из зависимости v=v(t). В сущности движение никогда не будет равномерным - такое движение предполагало бы постоянство скорости, чего никогда нет. Эта скорость лишь будет асимптотически сремится к 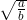 при при 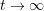 . Физически это означает, что по прошествии достаточно большого времени движение станет практически равномерным. . Физически это означает, что по прошествии достаточно большого времени движение станет практически равномерным.
Другое дело если Вы укажете степень точности, с которой измерятеся скорость. В этом случае можно указать нижнюю границу для такого момента времени t, после которого поправка к скорости будет сравнима с допустимой погрешностью её измерения.
Для пути также получена формула зависимости от времени. Первый член в этой формуле линеен по времени t; второй, нелинейный член, при больших t практически не зависит от времени и равен постоянной 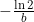 . Физически можно было бы сказать, что в начале своего движения тело двигалось неравномерно; по прошествии большого количества времени зависимость пройденного пути от времени практически "выродилась" в линейную: . Физически можно было бы сказать, что в начале своего движения тело двигалось неравномерно; по прошествии большого количества времени зависимость пройденного пути от времени практически "выродилась" в линейную:
%20%5Csimeq%20%5Csqrt{%5Cfrac{a}{b}}%5C%20t%20%5C%20-%20%5Cfrac{%5Cln2}{b}.)
(Сообщение отредактировал MEHT 16 апр. 2012 16:18)
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 16 апр. 2012 16:18 | IP
|
|
ellina1111

Новичок
|
     
ПОМОГИТЕ РЕШИТЬ ЗАДАЧУ ПОЖАЛУЙСТА!!! уходящие газы котельной установки проходят через воздухоподогреватель. начальная температура газов 300 градусов, конечная 141 градус. расход гахов равен 1090 кг\ч. начальная температура воздуха 15 градусов, а расход его равен 990 кг\ч. определить температуру нагретого воздуха если потери тепла в воздухоподогревателе составляет 4%. среднии теплоёмкости для газов и воздуха принять равными 1,0467 и 1,0048.
|
Всего сообщений: 1 | Присоединился: апрель 2012 | Отправлено: 16 апр. 2012 17:48 | IP
|
|
and27

Новичок
|
    
Цитата: MEHT написал 16 апр. 2012 15:55
Цитата: and27 написал 16 апр. 2012 11:43
А можно остановиться на втором выражении, когда у нас есть зависимость времени от скорости и найти константу?
А какой смысл? Это константа в промежуточных выкладках. Цель была найти скорость как функцию времени, разрешив соответствующее диф. уравнение.
Цитата: and27 написал 16 апр. 2012 12:49
Если в начальный момент времени t=0, то и путь должен быть раен нулю. Но из последнего выражения путь равен некоторой величине. Она ничтожна мала, если b большое число, но тем немение...прокоментируйте.
А он нулю и равен  С чего Вы взяли что это не так? С чего Вы взяли что это не так?
В первом члене понятно - он линеен по t; во втором члене экспонента в нулевой степени даст единицу, всё выражение под знаком логарифма следовательно тоже единица, ну а логарифм единицы 0.
А если мне нужна зависимость времени от скорости, я могу пользоваться вторым уравнениям?
|
Всего сообщений: 23 | Присоединился: апрель 2012 | Отправлено: 16 апр. 2012 19:10 | IP
|
|
|

 Форум
Форум

 Физика
Физика

 Задачи по физике для вузов
Задачи по физике для вузов

 Форум
Форум

 Физика
Физика

 Задачи по физике для вузов
Задачи по физике для вузов