Физика → Чертов, Воробьев → Примеры решения задач →
Физика твердого тела → §49 Элементы кристаллографии → Пример №1

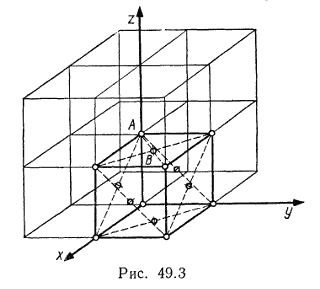
Выделим элементарную ячейку в кубической решетке (рис. 49.3) и определим, скольким соседним элементарным ячейкам принадлежит тот или иной узел выделенной ячейки. В этой ячейке имеются узлы двух типов: А (находящиеся в вершинах куба) и В (находящиеся на гранях куба в точке пересечения диагоналей).

Узел А принадлежит одновременно восьми элементарным ячейкам. Следовательно, в данную ячейку узел А входит с долей 1/8. Узел В входит одновременно только в две ячейки и, следовательно, в данную ячейку узел В входит с долей 1/2. Если учесть, что число узлов типа А в ячейке равно восьми, а число узлов типа В равно шести, т. е. числу граней, то общее число узлов, приходящихся на одну элементарную ячейку в гранецентрированной решетке,

n = (1/8)*8 + (1/2)*6 = 1 + 3 = 4 узла.

Так как число узлов равно числу атомов, то в соответствующей структуре на элементарную ячейку приходится четыре атома.